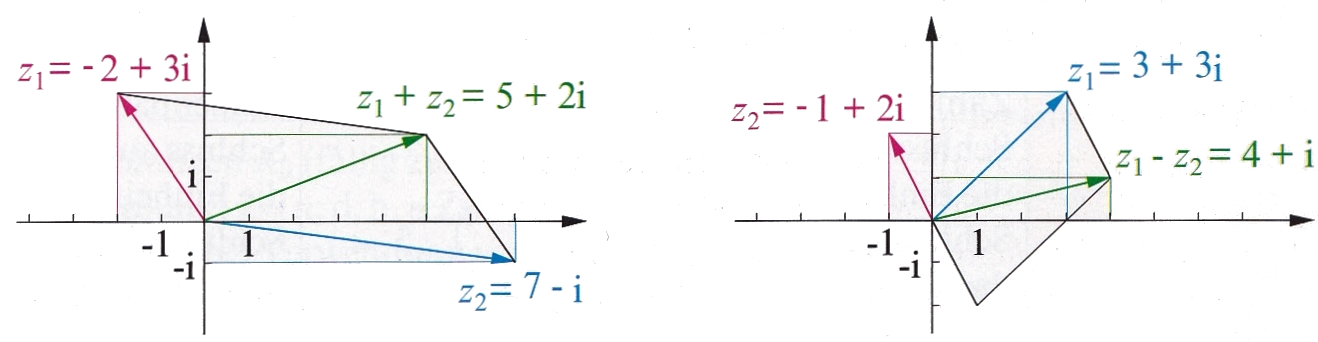| Ausführbarkeit von Rechenoperationen | Darstellung auf einer Zahlengeraden |
Natürliche Zahlen 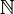 | Addition und Multiplikation sind stets ausführbar. Subtraktion und Division nicht immer. | Den natürlichen Zahlen entsprechen einzelne Punkte im Abstand von 1 auf dem Zahlenstrahl (ab 0). Jede Zahl (außer 0) hat einen Vorgänger und einen Nachfolger. |
Ganze Zahlen  | Addition, Subtraktion und Multiplikation sind stets ausführbar, Division nicht immer. | Den ganzen Zahlen entsprechen einzelne Punkte im Abstand von 1 auf der Zahlengeraden. Jede Zahl (auch 0) hat einen Vorgänger und einen Nachfolger. Die zu einer Zahl a entgegengesetzte Zahl ist -a (durch Punktspiegelung von a an 0) |
Bruchzahlen   0 0 | Addition, Multiplikation und Division (außer durch 0) sind stets ausführbar, Subtraktion nicht immer. Bruchzahlen können auch durch (endliche bzw. periodische) Dezimalbrüche dargestellt werden. | Die gebrochenen Zahlen liegen dicht auf dem Zahlenstrahl (ab 0), es gibt aber Punkte, zu denen keine gebrochene Zahl gehört (Lücken auf der Zahlengeraden). |
Rationale Zahlen  | Addition, Subtraktion, Multiplikation und Division (außer durch 0) sind stets ausführbar, Wurzelziehen nicht immer( Wurzeln die nicht als Bruchzahl darstellbar sind). | Die rationalen Zahlen liegen dicht auf dem Zahlenstrahl (ab 0), es gibt aber Punkte, zu denen keine rationale Zahl gehört (Lücken auf der Zahlengeraden). |
Reelle Zahlen 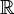 | Addition, Subtraktion, Multiplikation und Division (außer durch 0) sind stets ausführbar, Wurzeln aus positiven, reellen Zahlen können stets gezogen werden. | Jedem Punkt auf der Zahlengeraden entspricht genau eine reelle Zahl. |
Komplexe Zahlen  | Addition, Subtraktion, Multiplikation und Division (außer durch 0) und Radizieren (Wurzelziehen) sind stets ausführbar. | Die komplexen Zahlen können nicht mehr auf einer Zahlengerade, sondern in der Gauß'schen Zahlenebene dargestellt werden. (siehe unten) |
Komplexe Zahlen:
| Komplexe Zahlen in Normalform |  |
| Rechenoperationen mit komplexen Zahlen in Normalform |  |
| Komplexe Zahlen in trigonometrischer Form | 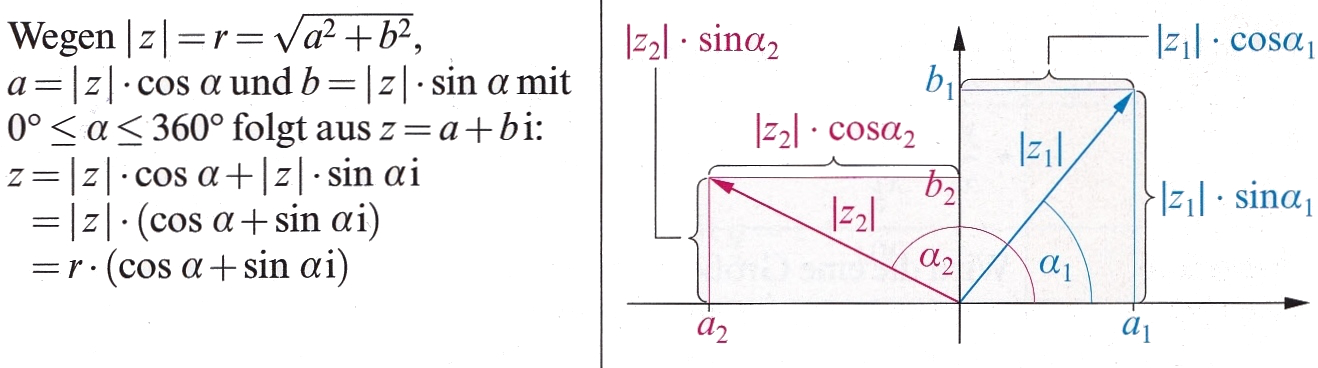 |
| Rechenoperationen mit komplexen Zahlen in trigonometrischer Form |  |
| Beispiel für die grafische Addition bzw. Subtraktion komplexer Zahlen | 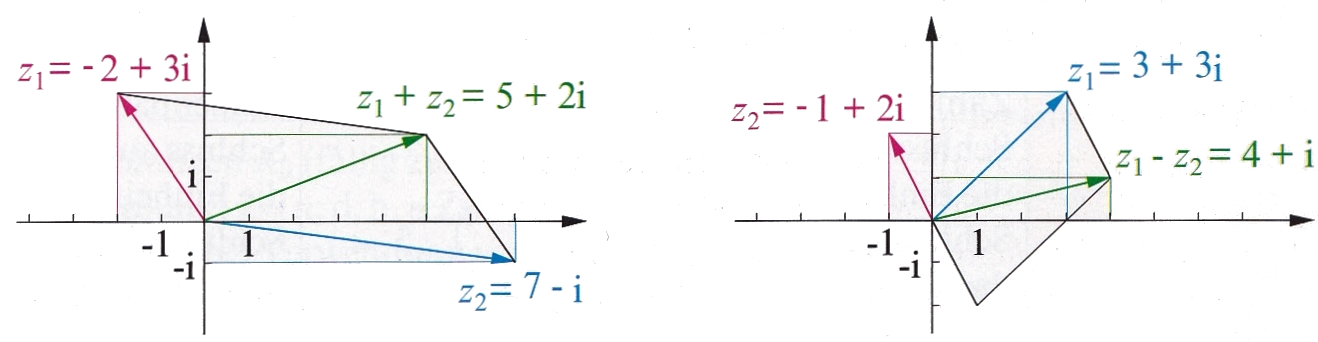 |
Quelle: "Das große Tafelwerk" Cornelsen Verlag