Induktion

Bewegte Leiter

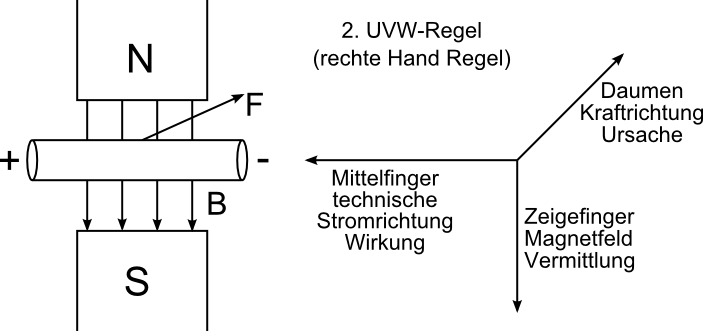
• durch die Kraft werden Ladungsträger bewegt
• auf bewegte Ladungsträger wirkt im Magnetfeld eine Kraft = Lorentzkraft
• Verschiebung der Ladungsträger ruft elektrisches Feld hervor

      F_L = F_el
Q·v·B = E·Q
homogenes elektrisches Feld E =
⇒ U = (-) B·v·l

mehrere Leiter:

Uind = -N·B·v·l mit v = Δs/Δt Uind = -N·B· Δs/Δt ·l Uind = -N·B· ΔA/Δt Uind = -N· Δ(B·A)/Δt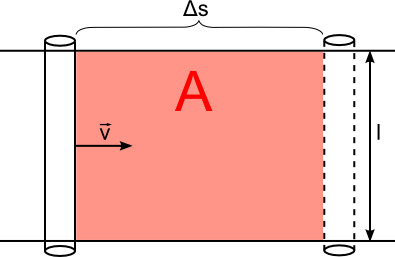

Magnetischer Fluss

Bei jeder Änderung des magnetischen Flusses Φ durch eine Leiterschleife oder Spule tritt eine Induktionsspannung U_ind auf.
U_ind = -N·
Formelzeichen: Φ
Einheit: Wb (Weber)1Wb = 1m²·1T = 1Vs
Gleichung: Φ = B·A

U_ind = -N·mit Φ(t) = B(t)·A(t)
folgt: U_ind = -N·(B(t)·A(t))
1. Ableitung:
U_ind = -N·(A·

dB(t)/dt

+B·

dA(t)/dt

)

A· dB(t)/dt	B· dA(t)/dt
Erzeugung einer Uind bei konstanter Fläche durch Änderung der Flussdichte (z.B. durch Änderung der Stromstärke) ⇒ Transformator	Erzeugung einer Uind bei konstanter magnetischer Flussdichte bei Änderung der Fläche ⇒ Generator

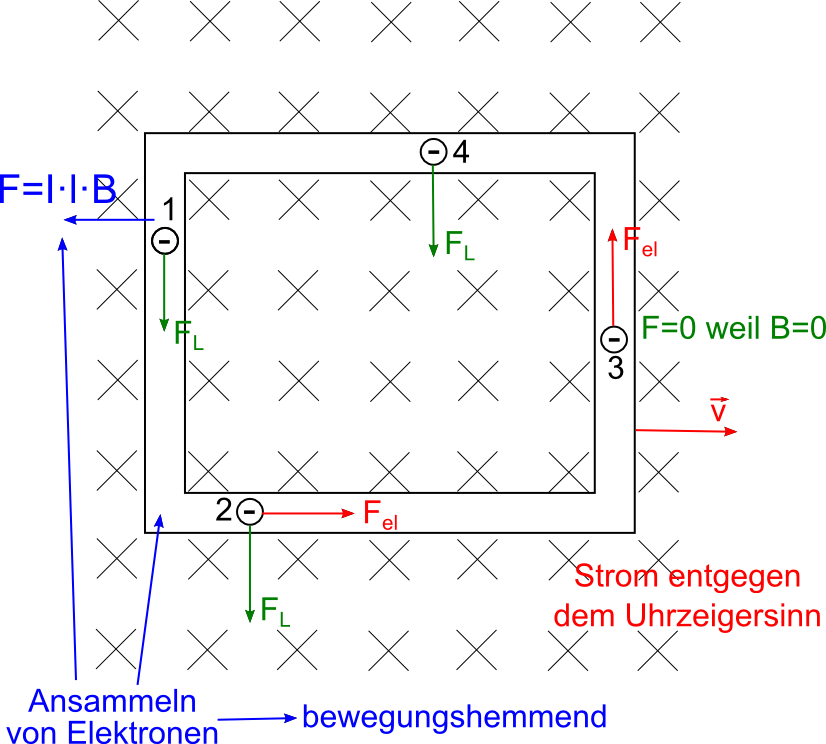
Generator

Herleitung:

U_ind = -N· =-N· =-N·(A· +B·)
Induktionsspannung durch Änderung der Fläche ≠ 0
bei konstantem Magnetfeld = 0
U_ind = -N·B·
Flächenänderung A(t) = A₀·cos φ
mit φ = ω·t          ω... Kreisfrequenz 2·π·f
U_ind = -N·B··A₀·cos (ω·t)
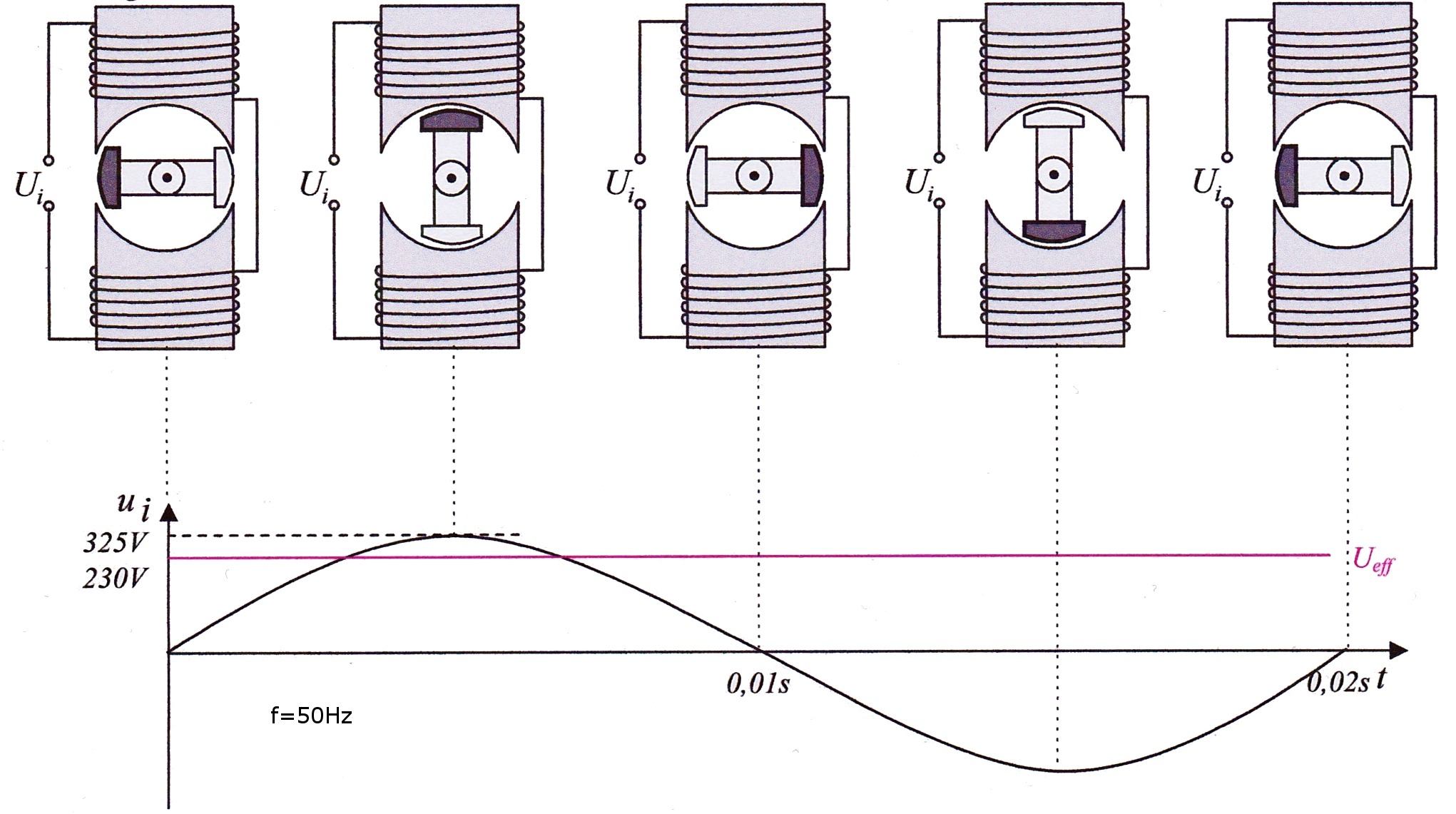
U_ind = -N·B·A₀··(cos (ω·t))
U_ind = N·B·A₀·ω·sin (ω·t)
U_ind = N·B·A₀·2·π·f·sin (ω·t)

Maximalspannung U_max = 2·π·f·N·B·A₀
f... Frequenz des Wechselstroms (Drehbewegung)
N... Windungszahl der Induktionsspulen
B... magnetische Flussdichte des Erregerfeldes
A₀... Fläche der Induktionsspulen

u(t) = U_max·sin (ω·t)
U_eff =

Leistung im Wechselstromkreis:

P(t) = u(t)·i(t) = U_max·I_max·sin² (ω·t)

Aufbau:

Rotor Stator Schleifringe oder Kommutator Kohlebürsten

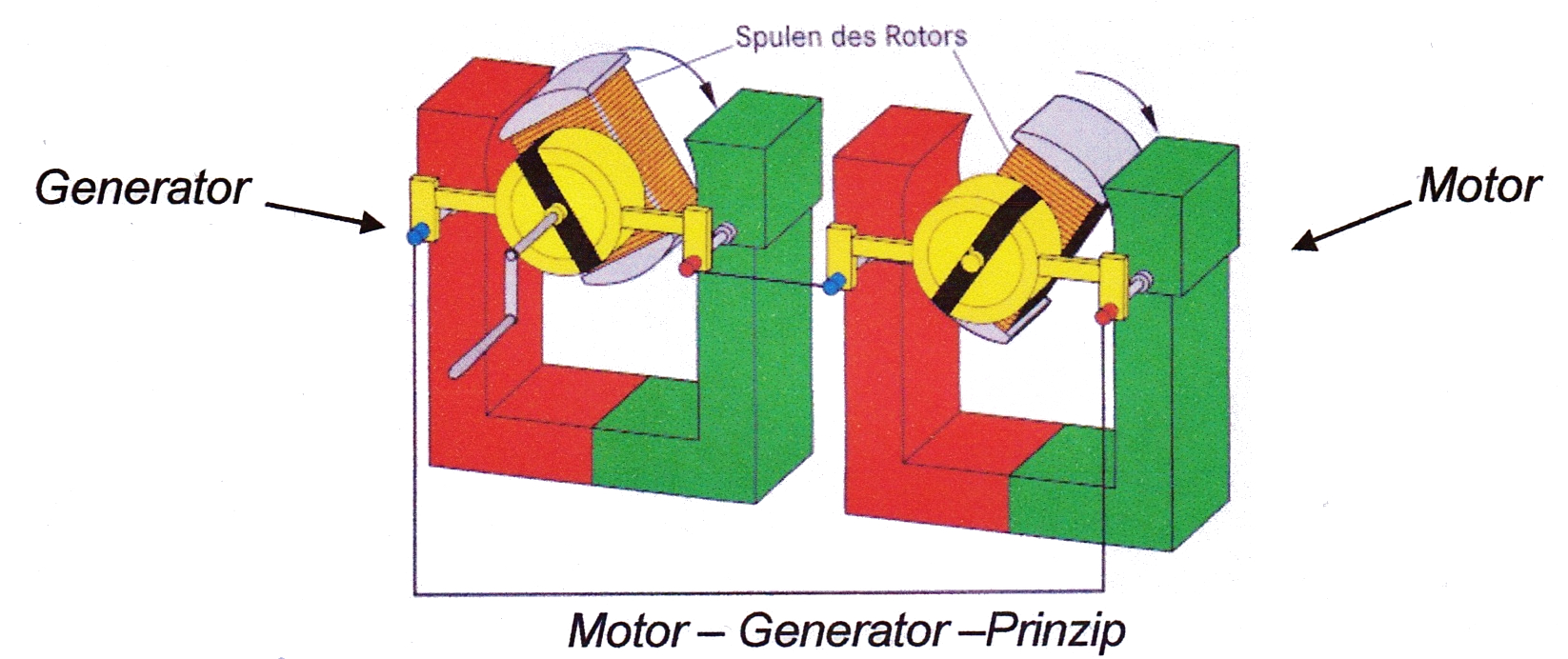Wirkungsweise über Anwendung des Induktionsgesetzes durch Veränderung der Fläche:

Transformator

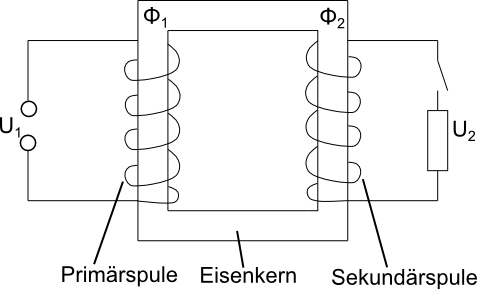
• Primärspule ⇒ Wechselspannung ⇒ Φ ändert sich ständig
• Φ durchsetzt auch Sekundärspule ⇒ Induktionsspannung
• idealer Transformator: R=0 ⇒ nicht belastet (Stromkreis auf Sekundärseite nicht geschlossen)
⇒
U₁(t)/U₂(t)
=
N₁/N₂
oder
U_{1 eff}/U_{2 eff}
=
N₁/N₂
• bei idealem Transformator im Kurzschlussfall gilt:
I_{1 eff}/I_{2 eff}
=
N₂/N₁
• in der Primärspule wird durch Selbstinduktion eine Sapnnung induziert, die der angelegten Spannung entgegenwirkt
• der sich periodisch ändernde Fluss Φ im Eisenkern führt zu einer Induktionsspannung U₂

Gesetzmäßigkeiten:

Spannungsübersetzung am idealen unbelasteten Transformator (R→∞)	U1/U2 = N1/N2
Stromstärkeübersetzung am idealen stark belasteten Transformator (R=0)	I1/I2 = N2/N1
Leistung am Transformator bei starker Belastung unter Vernachlässigung aller Verluste (Φ1 = Φ2)	U1·I1 = U2·I2

Energieumwandlung:

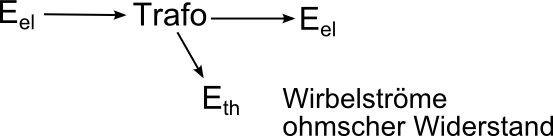
Wirkungsgrad:

η = =

Lenzsches Gesetz

Energieerhaltungssatz bei elektromagnetischer Induktion

vor		nach
0	=	Emech + Eel
0	=	F·Δs+Q·Uind
⇒ Uind = - F·Δs/Q		Kraft entspricht Lorentzkraft F = B·I·l
Uind = - B·I·l·Δs/I·Δt	=	- B·ΔA/Δt

Lenzsche Regel:

Der Induktionsstrom (und damit Spannung; wirkende Kräfte) sind stets so gerichtet, dass sie der Ursache der Entstehung entgegenwirken.

Wirbelströme

zeitlich konstantes Magnetfeld	zeitlich veränderliches Magnetfeld
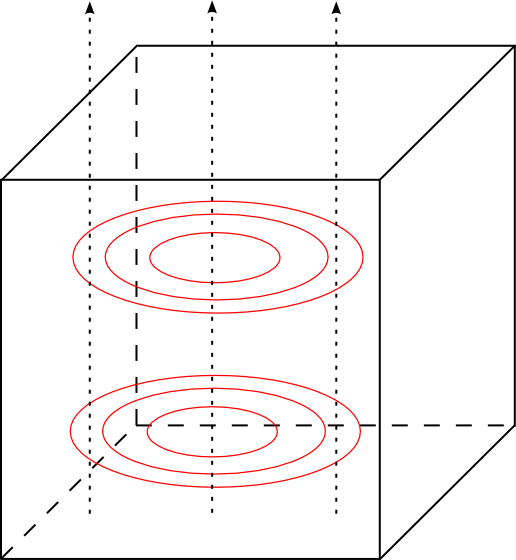Wirbelströme sind abhängig von der Bewegungsrichtung und der Richtung des Magnetfeldes	Wirbelströme sind abhängig von der Änderungsrichtung der magnetischen Flussdichte und der Richtung des Magnetfeldes

Wirbelströme entstehen in massiven metallischen Leitern, wenn sich das umfasste magnetische Feld ändert. Wirbelströme können durch Blätterung vermieden werden.

Wirbelströme sind:

erwünscht	unerwünscht
Wirbelstrombremse Oberflächenhärten Tachometer kWh-Zähler Induktionsherd	Motor Generator Transformator

Selbstinduktion

U_ind = -N·A· =-μ_r·μ₀··A·
U_ind = -L·     mit      L = μ_r·μ₀··A

• Induktionsspannung als Folge der Verringerung des magnetischen Flusses (beim Ausschalten)
• ansteigender Strom ⇒ magnetischer Fluss nimmt zu (Einschalten)
• ⇒ Induktionsspannung wirkt diesem Vorgang entgegen
• Stromstärke erreicht erst allmählich Höchstwert
• lange dünne Spule: B = μ_r·μ₀·
  N·I/l

Induktivität L

Die Induktivität einer Spule gibt an, wie stark die Änderung der Stromstärke in der Spule aufgrund der Selbstinduktion behindert wird.
Formelzeichen: L
Einheit: H (Henry)

Die Induktivität einer langen Spule kann mit folgender Gleichung berechnet werden:L = μ_r·μ₀··A
U_ind = L·

Interpretation:

physikalische Größen:
A... Querschnittsfläche der Spule
l... Länge der Spule
N... Windungszahl der Spule
μ_r... Permeabilitätszahl
μ₀... magnetische Feldkonstante

Zusammenhänge:
L∼A: je größer A desto größer L
L∼N²: bei doppelter N vervierfacht sich L
-indirekte Proportionalität zur l
-Induktivität ist vom Stoff in der Spule abhängig
-Gültigkeitsbedingungen: lange, dünne Spule

Wechselstromkreis

Ohmsches Bauelement:

Durch Wechselwirkung zwischen Elektronen und Metallgitter entsteht der ohmsche Widerstand.
R =

U/I

R_∼ = R₋

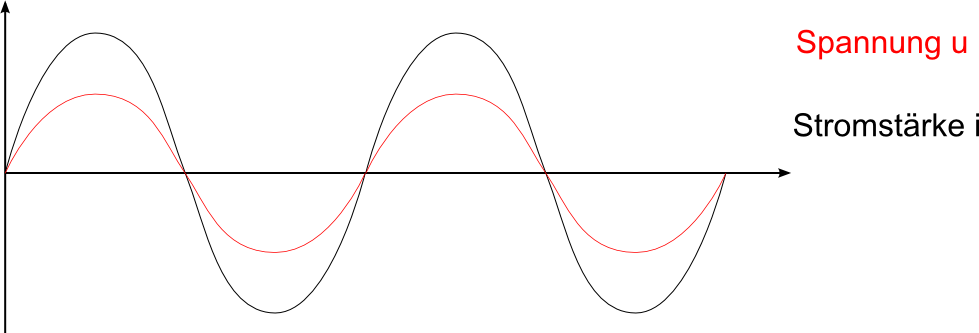
Spannung und Stromstärke verlaufen zeitgleich
E_el → E_th
Der Spannungsquelle wird Energie entnommen.
Anmerkung: R₋ = Z... Scheinwiderstand im Wechselstromkreis

Spulen:

Durch Selbstinduktion in der Spule entsteht ein induktiver Widerstand.
X_L = 2·π·f·L
X_L... induktiver (Blind-)Widerstand

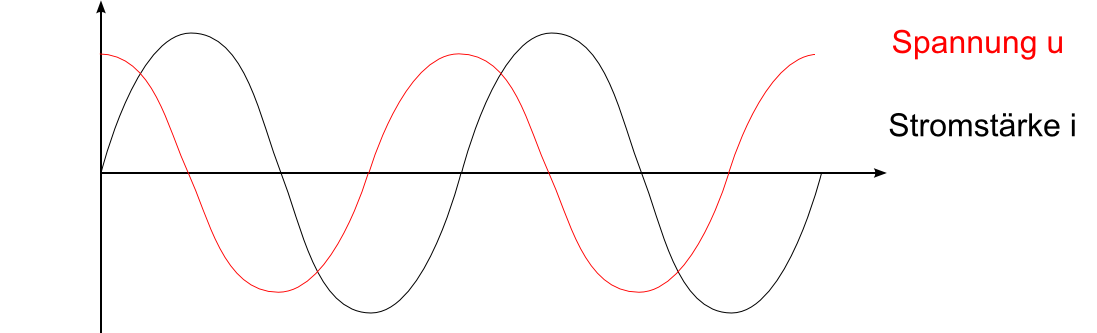
                     E_el ←→ E_{magn. Feld}
Spannungsquelle          Spule
Die Stromstärke eilt der Spannung hinterher
Der Spannungsquelle wird keine Energie entnommen.

Kondensatoren:

Im Gleichstromkreis ist der Stromfluss unterbrochen.
Durch die begrenzte Aufnahmefähigkeit des Kondensators für elektrische Ladungen entsteht der kapazitive Widerstand.
X_C =

1/2·π·f·C

X_C... kapazitiver (Blind-)Widerstand

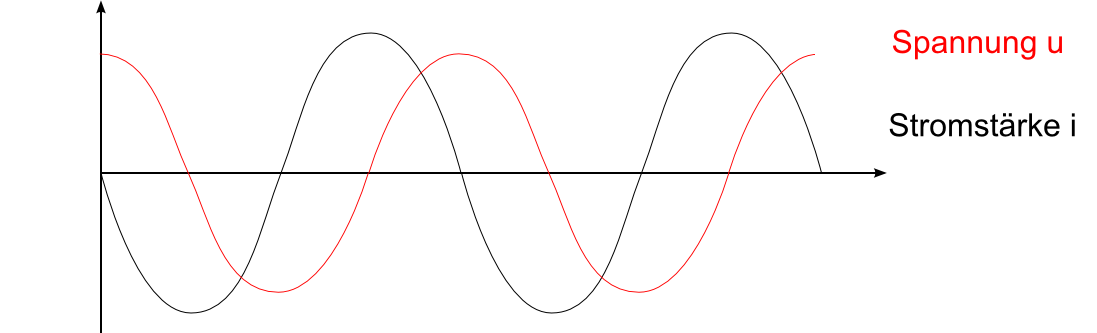
                     E_el ←→ E_{el. Feld}
Spannungsquelle          Kondensator
Die Stromstärke eilt der Spannung voraus.
Der Spannungsquelle wird keine Energie entnommen.

Hoch- und Tiefpass:

Hochpass	Tiefpass

Leistung im Wechselstromkreis:

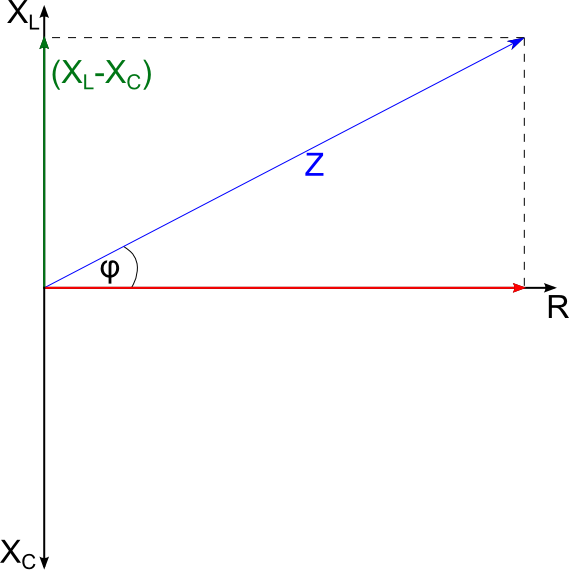Z = √R2+(XL-XC)2 Z = U/I = √R2+X2 φ... Phasenverschiebung zwischen U und I cos φ... Leistungsfaktor; cos φ ≤ 1

Es ist zwischen der Wirkleistung, der Blindleistung und der Scheinleistung zu unterscheiden.

Die Wirkleistung ist die im Wechselstromkreis an ohmschen Widerständen (Wirkwiderständen) "nach außen" umgesetzte Leistung.

Die Blindleistung ist die in den Blindwiderständen X_L und X_C kurzzeitig zum Aufbau des magnetischen bzw. elektrischen Feldeserforderliche Leistung, die beim Abbau der Felder wieder an den Stromkreis abgegeben wird. Ihr zeitlicher Mittelwert ist daher null.

Wirkleistung P P = U·I·cos φ Blindleistung Q Q = U·I·sin φ Die Scheinleistung S erhält man damit zu: S = √P2+Q2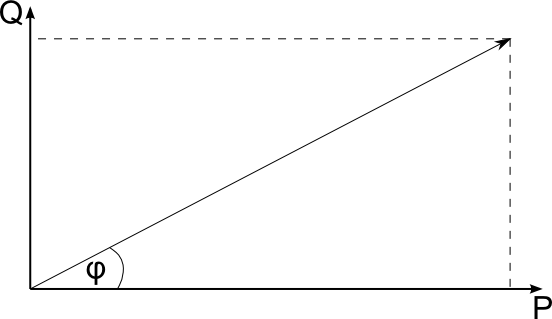

Leitungsvorgänge in Metallen und Halbleitern

Teilchenaufbau

Bändermodell

Elektronen im Metallgitter frei beweglich (ortsfeste positive Ladungen) in Halbleitern: bei Energiezufuhr → zusätzliche e- werden frei → jedes e- hinterlässt Elektronenfehlstelle → kann durch e- des Nachbaratoms besetzt werden Temperaturabhängigkeit in Metallen: R = θ· l/A = θ· l0·(1+α·ΔT)/A = R0·(1+α·ΔT) θ = 1/n·e·μ Driftgeschwindigkeit: vD = UH/b·B in Halbleitern: je höher T, desto größer e--Anzahl

Valenzband: voll besetzt Leitungsband: teilweise besetzt, Abstand und Besetzung entscheiden über elektrische Leitfähigkeit En = k·13,6eV· Z2/n2 rn = k·a0·n2