Eigenschaften ruhender Ladungen
Eigenschaften von Ladungen:
- positive (Elektronenmangel) und negative (Elektronenüberschuss) Ladungen
- sind trennbar
- sind übertragbar
- gleiche Ladungen Stoßen sich ab
- unterschiedliche Ladungen ziehen sich an
- Kraftwirkung auf ungeladene Körper
| Metalle | Isolatoren |
| Influenz | Polarisation |
| Ladungstrennung unter Einfluss eines anderen geladenen Körpers aufgrund von Kraftwirkungen | Ladungsträgerverschiebung im mikroskopischen Bereich |
Ladungstrennung:
Durch Ladungstrennung entstehen aus elektrisch neutralen Körpern positiv geladene Körper und negativ geladene Körper.Ladungstrennung erfolgt durch:
- Reibung
- Wärme
- Strahlung
Nachweisgeräte:
- Elektroskop
- Glimmlampe
Physikalische Größe Ladung
Die Ladung eines Körpers gibt an, wie groß sein Elektronenüberschuss bzw. sein Elektronenmangel ist.Formelzeichen: Q
Einheit: 1C = 1A·s
Coulomb'sches Gesetz: F =
14·π·εQ·εr
-Q1·Q2r2
εQ... elektrische Feldkonstante 8,8541878·10-12 C·V-1·m-1
εr... Permittivitätszahl oder Dielektrizitätszahl (Luft ≈ 1)
Q1, Q2... elektrische Ladungen der Körper in C
r... Abstand der Massenmittelpunkte
Bestimmung der Elementarladung e:
2. Faraday'sches Gesetz: Q = n·z·Fn... Stoffmenge (kmol)
z... Wertigkeit
F... Faradaykonstante = 9,6485·107
Ckmol
- für die Stoffmenge 1kmol eines einwertigen Ions ist die Ladung 9,6485·107 C nötig
- 1kmol enthält 6,022·1026 Teilchen (Avogadro-Konstante)
9,6485·107 C6,022·1026
=1,602·10-19 CDas elektrische Feld
Im Raum um geladene Körper besteht ein elektrisches Feld. Ein elektrisches Feld erkannt man an den Kräften auf (un)geladenen Körpern.Elektrische Felder lassen sich mit Hilfe von Feldlinien(elektrische Kraftlinien) veranschaulichen:
- Kraft nach Coulomb'schen Gesetz von jeder Ladung auf Probeladung berechnen
- vektorielle Kräfteaddition
Feldlinienbilder:
| radiales Feld einer positiven Ladung | radiales Feld einer negativen Ladung | homogenes Feld (parallele Feldlinien) | inhomogenes Feld (nichtparallele Feldlinien) |
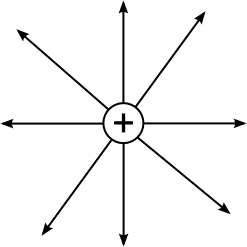 | 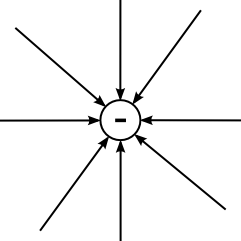 | 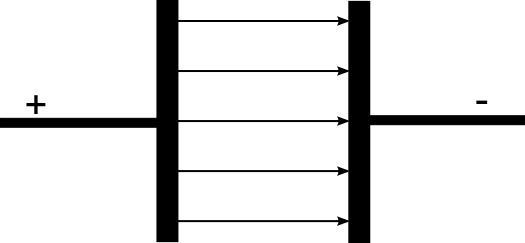 | 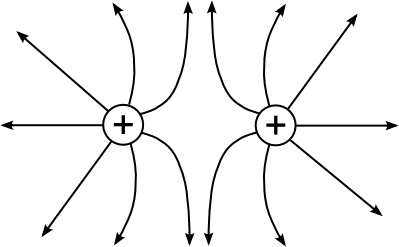  |
Die Feldlinien...
- geben an jedem Punkt des elektrischen Feldes die Richtung der dort wirkenden elektrostatischen Kraft an
- verlaufen von der positiven Ladung zur negativen Ladung
- beschreiben die Bewegung einer positiven Probeladung im elektrischen Feld
- treten senkrecht aus der Oberfläche eines geladenen Körpers auf
- überschneiden sich nicht
Die elektrische Feldstärke
Die elektrische Feldstärke in einem Punkt gibt an, wie groß die Kraft je Ladung in diesem Punkt ist.Formelzeichen: E
Einheiten:
NC
;Vm
Gleichung: E =
FQ
F... Kraft auf einen positiv geladenen Körper
Q... Ladung dieses Körpers (Probeladung)
umgestellt nach der Kraft: Fel = Q·E
Für das homogene Feld im Inneren eines Plattenkondensators kann die elektrische Feldstärke berechnet werden mit der Gleichung:
E =
Ud
U... Spannung zwischen den Platten
d... Abstand der Platten
für Radialfelder folgt aus dem Coulomb'schen Gesetz:
E =
14·π·εQ·εr
-Q1r2
Q1... felderzeugende Ladung
r... Abstand von der felderzeugenden Ladung
Kondensator
- 2 elektrisch leitende Körper durch Isolator getrennt
- Anschluss an elektrische Quelle ⇒ Kondensator wird geladen
- Lösen von elektrischer Quelle ⇒ Ladung bleibt erhalten
- Kapazität C des Kondensators: C =QU=QE·d=ε0·Ad=ε0·εr·Ad
- Einheit der Kapazität: 1CV= 1F (Farad)
- E' = 1εr·E
- Parallelschaltung: Q = Q1+Q2 = C1·U+C2·U
CErtsatz = C1+C2 - Reihenschaltung: U = U1+U2 = QC1+QC21CErsatz1C1+QC2
Entladekurve eines Kondensators:
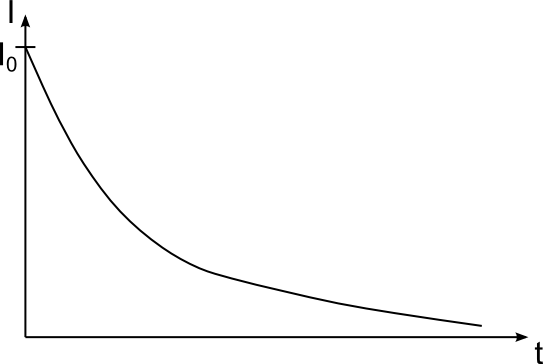
Funktionsgleichung: y = f(x) = a·e-bx
I(t) = I0·e-kt
k... Entladekonstante
k =
1R·C
Die Fläche unter der Kurve ist ein Maß für die gespeicherte Ladung Q:
Q = ∫ I(t)dt
wenn I = konstant folgt: Q = I·t
Gespeicherte Energie im Kondensators:
Vergleich Mechanik: Fläche im F(s)-Diagramm war ein Maß für die verrichtete Arbeit und damit der Energieänderung.W = F·s = E·Q·s = Q·U wenn Fel = konstant
Interpretation: Die Fläche unter der Kurve im U(Q)-Diagramm ist ein Maß für die gespeicherte elektrische Energie im Kondensator.
Eel =
12
·Q·U mit Q = C·U folgt:Eel =
12
·C·U2Arbeit und Energie im elektrischen Feld
- allgemein: die Fläche im F(r)-Diagramm ist ein Maß für die verrichtete Arbeit
- jeder geladene Körper hat im elektrischen Feld potenzielle Energie
- ΔEpot = W = ∫ F dr