Quantenphysik

Der äußere Lichtelektrische Effekt (Photoeffekt)

1. Experiment (qualitativ):

Eine negativ geladene Zinkplatte wird mit UV-Licht bestrahlt. Licht als elektromagnetische Welle (so dachte man) versetztElektronen in Schwingung bis sie sich aus dem Metall ablösen.

Beobachtung:

Das Elektroskop zeigt abnehmende Ladung an. Schiebt man eine Glasplatte ein, so erfolgt keine Entladung.

Erklärung:

  • nach Wellentheorie: Elektronen von Lichtwelle zu Schwingung angeregt
  • größte Lichtintensität ⇒ elektrische Feldstärke größer
  • Elektronen sollen mit größerer Amplitude schwingen ⇒ werden leichter aus Metall abgelöst

Widerspruch zu den Beobachtungen:

  • bei Bestrahlung mit sichtbarem Licht ⇒ keine Elektronen abgelöst
  • selbst wenn man die Intensität sehr stark erhöht
  • nur hochfrequentes UV-Licht löst Elektronen aus (selbst bei sehr niedriger Intensität)
⇒ Die Wellentheorie des Lichts gerät in Erklärungsschwierigkeiten


2. Experiment (quantitativ): Gegenfeldmethode


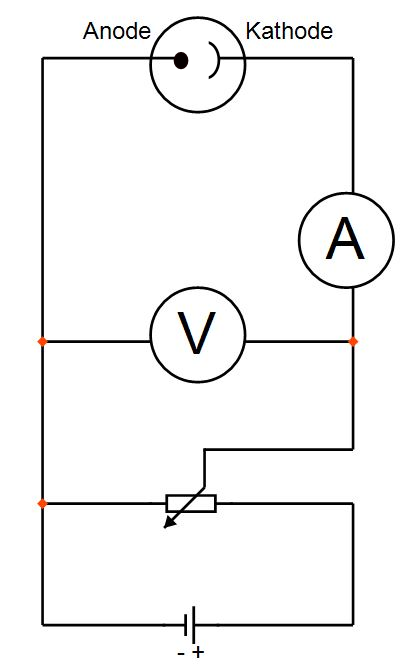Durch Licht einer Quecksilberspektralröhre wird die Fotokathode bestrahlt. Das Licht wird durch ein Gitter in seine Spektrallinien zerlegt. Es werden wie beim 1. Experiment Elektronen aus der Kathode herausgelöst. Diese gelangen zur Anode. Nun wird die Spannung solange erhöht bis kein Elektron die Anode erreicht (I = 0). Dazu ist an der Photozelle eine veränderliche Gegenspannung angelegt.

Messwerttabelle:

Farbe Wellenlänge
λ in nm		 Frequenz
f in 1014Hz		 Gegenspannung
U in V		 kinetische Energie
Ekin in 10-19J
gelb 578 5,187 0,4 0,64088
grün 546 5,491 0,55 0,88121
blau 491 6,106 0,85 1,36187
indigo 436 6,876 1,05 1,68231
violett 405 7,402 1,35 2,16297

Gleichungen:

c = λ·f
Eel = e·U=Ekin



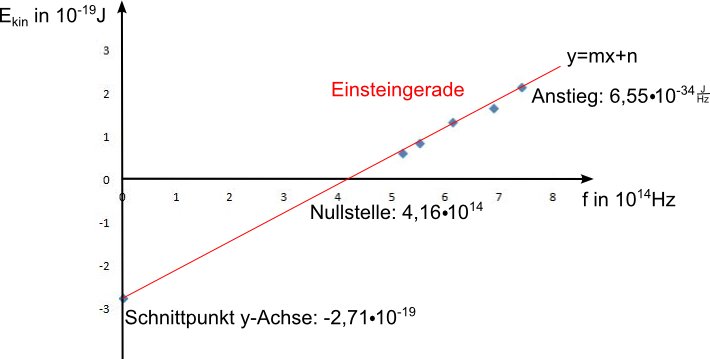
Ergebnisse des Experiments:

  1. Licht ab einer bestimmten Frequenz kann aus Metallen Elektronen herauslösen.
  2. Die kinetische Energie der ausgelösten Elektronen ist unabhängig von der Beleuchtungsstärke.
  3. Die beim Fotoeffekt auf ein ausgelöstes Elektron übertragene Energie wächst mit der Frequenz direkt proportional

Deutung nach Einstein:

Ekine + WA = ELicht
      Elektron    Licht
      Teilchen    Welle Teilchen

Licht zeigt Teilcheneigenschaften

Energiebetrachtung

Ekine = m·f - WA
Ekine... kinetische Energie der Elektronen
m... Anstieg der Geraden
WA... Austrittsarbeit der Elektronen

Anstieg = Plancksches Wirkungsquantum h=6,62·10-34Js
Ekine + WA = ELicht

Metalle X, Y und Z mit WAX > WAY > WAZ


Energie des Lichts: E = h·f
Entweder gibt Licht seine gesamte Energie an das Elektron ab, oder es passiert nichts!

Einstein: E = m· c2 folgt
Masse des Lichts: m =
h·f/c2

Impuls des Lichts: p = m·c =
h·f/c2
·c =
h·f/c
mitf =
c/λ
folgtp =
c/λ


Es ergeben sich folgende Ergebnisse:

  1. die klassischen Teilchen Elektronen zeigen auch Wellencharakter (Materiewelle/ de Broglie-Wellen ⇒ Beugung)
  2. die klassische elektromagnetische Welle Licht zeigt auch Teilchencharakter (Photon ⇒ Impuls)
Beide Eigenschaften finden eine Vereinigung durch das Plancksche Wirkungsquantum in der Formel h = p·λ
Dieses oft unter dem Begriff "Dualismus" subsummierte nicht mehr klar unterscheidbare Verhalten von Welle und Teilchen imMikrokosmos ist ein wesentliches Kennzeichen der Quantenphysik. Deshalb fasst man die Mikroobjekte auch als "Quanten"zusammen, die alle ein ähnliches Verhalten zeigen.

Eigenschaften von Quantenobjekten:


Im Unterschied zu den uns umgebenden makroskopischen Körpern gilt für Quantenobjekte:
  • Quantenobjekte bewegen sich nicht auf Bahnen
  • Quantenobjekte sind keine kleinen Kügelchen
  • bei Quantenobjekten treten Teilchen- und Welleneigenschaften auf
Quantenobjekte haben etwas...
  • Welliges, was ihre Ausbreitung bestimmt und z.B. auch Interferenz bewirkt
  • Körniges oder Teilchenhaftes, was sich z.B. bei einer Ortsmessung zeigt
  • Stochastisches, was keine Aussage über das Verhalten eines einzelnen Quantenobjekts erlaubt, wohl aber Wahrscheinlichkeitsaussagen für eine große Anzahl von Quantenobjekten

Taylor-Experiment:

  • Beugung und Interferenz sind nicht abhängig von der Lichtintensität
  • je höher die Intensität ⇒ Welleneigenschaften
  • je niedriger die Intensität ⇒ Teilcheneigenschaften

Vergleich Lichtmikroskop - Elektronenmikroskop:


Lichtmikroskop Elektronenmikroskop
Das Objekt wird mit Licht durchstrahlt Das Objekt wird mit schnell bewegten Elektronen durchstrahlt
Die Abbildung erfolgt durch optische Linsen (Nutzung der Brechung von Licht) Die Abbildung erfolgt durch Magnetlinsen (Nutzung der Ablenkung von Elektronen in Magnetfeldern)
Es entsteht ein vergrößertes Bild des Objekts, das mit den Augen betrachtet oder fotografiert werden kann Es entsteht ein vergrößertes Bild des Objekts, das mit den Augen betrachtet oder fotografiert werden kann
Meist wird mit 20facher bis 1000facher Vergrößerung gearbeitet Die Vergrößerung ist etwa um den Faktor 103 größer als bei einem Lichtmikroskop
Das Auflösungsvermögen ist durch die Wellenlänge des Lichts begrenzt (bei blauem Licht 0,4µm) Das Auflösungsvermögen ist durch die Beschleunigungsspannung begrenzt (bei 100kV ⇒ 0,3nm)

Das Bohrsche Atommodell

Planetenmodell (Rutherford 1911):

Elektronen kreisen auf beliebigen Bahnen mit beliebiger Neigung um den positiven Atomkern.
Coulombkraft FQ = Zentrifugalkraft FZ
(1)
1/2·π·ε0
·
e2/r2
=
m·v2/r

unverstanden bei diesem Modell sind:
  • die stabilen Kreisbahnen, da die negativ geladenen Elektronen unter Abgabe von Strahlung innerhalb kürzester Zeit in den Kern stürzen würden
  • die Spektrallinien

Bohrsches Atommodell (1913):

1.Postulat:

Das Atom hat eine Anzahl stationärer, d.h. strahlungsarmer Zustände. In jedem dieser Zustände hat es einen bestimmten Energiegehalt En
(2) me·vn·2·π·rn = n·h         Bohrsche Quantenbedingung
n... Hauptquantenzahl     n=1, 2, 3, ...
Die Wirkung des umlaufenden Elektrons ist gleich einem ganzzahligen Vielfachen von h.

2.Postulat:

Der Übergang von einem dieser Zustände En zu einem anderen Em erfolgt sprunghaft unter Aufnahme bzw. Abgabe eines Lichtquants: Quantensprung
Daraus folgt mit der Energie für ein Lichtquant: E = h·f
h·f = Em - En         Bohrsche Frequenzbedingung

Das erste Postulat gilt nur, wenn die elektrostatische Anziehungskraft gleich der Radialkraft ist. Aus Gleichung (1) folgt:
(3)
e2/4·π·ε0
=me·v2·rn

Aus der Bohrschen Quantenbedingung folgt für die Bahngeschwindigkeit vn:
(4)
n·h/2·π·me·rn


Diese Gleichung quadriert und in Gleichung (3) eingesetzt ergibt:
(5)
e2/4·π·ε0
=
n2·h2/4·π2·me·rn


Umgestellt nach dem Bahnradius ergibt sich:
(6) rn =
ε0·h2/π·e2·me
·n2 =5,29·10-11m·n2

Gleichung (6) in Gleichung (4) eingesetzt ergibt die Geschwindigkeit des Elektrons im Grundzustand eines Wasserstoffatoms:
vn =
e2/2·ε0·h
·
1/n
= 2,19·106
m/s
·
1/n


Die Energie des Elektrons auf einer Bahn ist die Summe aus der
kinetischen Energie: Ekin =
1/2
·m·v2 =
1/2
·me·
e4/4·ε02·h2
·
1/n2
=
e4·me/8·ε02·h2
·
1/n2

und potenziellen Energie ("Hubarbeit"): Epot = Fel·r =
1/4·π·ε0
·
e2/r2
·r =-
e2/4·π·ε0·rn
=-
e2·π·e2·me/4·π·ε0·ε0·h2·n2
=-
1/4
·
e4·me/ε02·h2
·
1/n2

Gesamtenergie: Ekin + Epot = -
1/8
·
e4·me/ε02·h2
·
1/n2


Berechnung der Energie des Elektrons im Grundzustand (n=1) E1 = -2,18·10-18J = -13,6eV für Wasserstoff
⇒ En = -13,6eV·
1/n2


Energieniveauschema für Wasserstoff:

Balmer Serie (teilweise sichtbar)
Lyman Serie (ultraviolett)
Paschen Serie (infrarot)

Emission:

  • Aussenden von Licht
  • Zufuhr von Energie ⇒ Stoff leuchtet ⇒ gibt Licht ab
  • Abgabe von Energie aus Atomhülle

Absorption:

  • Aufnahme von Energie
  • jeder Stoff absorbiert Licht mit derselben Wellenlänge, mit der er Licht emittiert ⇒ Absorptionsspektrum

Serienformel für Wasserstoff:

f = fRy·(
1/m2
-
1/n2
)
fRy... Rydbergfrequenz         fRy=3,28984195·1015Hz
EPhoton = h·fRy·(
1/m2
-
1/n2
)
EPhoton = 13,6eV·(
1/m2
-
1/n2
)
En = -h·Ry·
1/n2
        in der Einheit J         fRy = Ry

Anregung durch:

Licht Teilchen (Elektronen)
ΔE = Em - En = h·f
vollständige Energieabgabe		 teilweise Energieabgabe

Arten von Spektren:

  • Kontinuierliches Spektrum:
    • glühende Festkörper, Flüssigkeiten und Gase unter hohem Druck
  • Linsenspektrum:
    • Gase unter geringem Druck
  • Absorptionsspektrum:
    • jeder Stoff kann genau die Wellenlänge absorbieren die er selbst aussenden würde
    • es kommt zur Anregung der Atome

Vorzüge und Mängel des Bohrschen Atommodells:


Vorzüge Grenzen
trägt als erstes Modell der Tatsache Rechnung, dass die klassische Physik Atome nicht richtig beschreiben kann im Rahmen der klassischen Physik sind Postulate unverständlich und erscheinen willkürlich
erklärt alle Emissions- und Absorptionsvorgänge richtig als Energieänderung der Valenzelektronen der klassische Begriff "Bahn" setzt genaue Kenntnis des Ortes voraus; Widerspruch zur Unschärferelation
Serienformel des Wasserstoffspektrums lässt sich sehr genau herleiten Widersprüche bei der Behandlung von Mehrelektronensystemen
Rydbergkonstante und Ionisierungsenergie des Wasserstoffs lassen sich durch Konstanten ausdrücken Gestalt des Wasserstoffatoms mittels Bohrscher Theorie eine Scheibe, keine Kugel
Spektren wasserstoffähnlicher Atome und Ionen lassen sich sehr genau berechnen keine Aussagen über Intensität oder Polarisation der vom Wasserstoff emittierten Strahlung
Durchmesser des Wasserstoffatoms wird größenordnungsmäßig richtig bestimmt liefert die magnetischen Eigenschaften nicht richtig

Einelektronensysteme

Wasserstoffatom 1H 1·e·e = 1e2
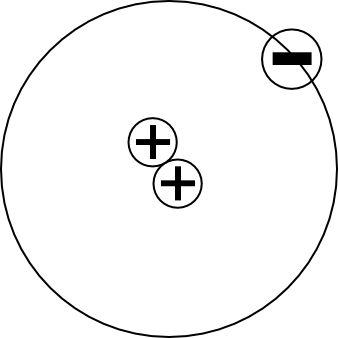Heliumion 2He+ 2·e·e = 2e2
Lithiumion (zweifach ionisiert) 3Li2+ 3·e·e = 3e2

Orbital:

Bereich der höchsten Aufenthaltswahrscheinlichkeit φ2 ⇒ jede Spektrallinie hat eine natürliche Breite

Lumineszenz:

  • = inverser Photoeffekt
  • Eel→ELicht
  • z.B. LED

Phosphoreszenz:

  • verzögerte Emission (in mehreren Stufen)
  • ⇒ Stoffe leuchten noch längere Zeit
  • Absorption energiereichen Lichts; kurzwellig → langwellig

Fluoreszenz:

  • kleinerer Energiebetrag emittiert als absorbiert
  • ⇒ dafür muss freies Energieniveau zur Verfügung stehen
  • ⇒ emittiertes Licht ist langwellig

Der Laser

prinzipieller Aufbau:

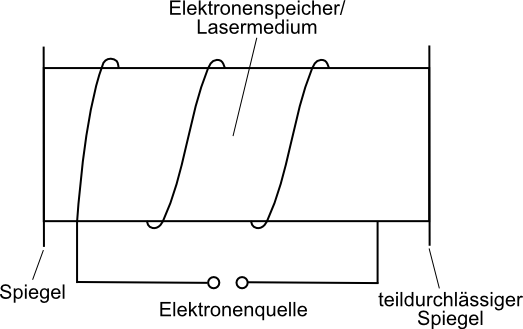Plattenkondensator mit isolierender Folie, dessen eine Platte geteilt ist
⇒ diese Teile sind mit hochohmigem Widerstand verbunden

Eigenschaften Laserlicht:

  • Laserlicht ist nahezu paralleles Licht
  • Laserlicht ist Licht einer Frequenz bzw. einer Wellenlänge (monochromatisches Licht)
  • Frequenz (λ, Farbe) hängt vom Lasermedium ab
  • Laserlicht kann eine hohe Leistungsdichte von bis zu einigen MWt/cm2 erreichen

spontane und induzierte Emission:


spontane Emission induzierte Emission
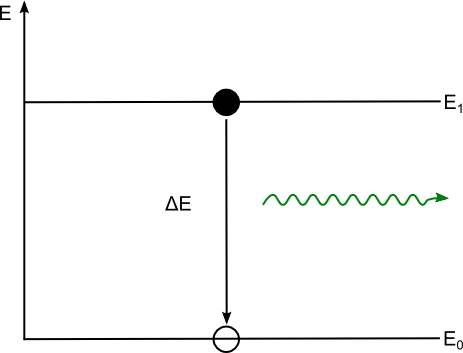Angeregter Zustand besteht nur ca. 10-8s. Die Emission erfolgt ohne äußere Einwirkung Angeregter Zustand besteht mehr als 10-2s. Die Emission wird durch Photonen stimuliert
z.B. glühender Wolframdraht z.B. Laser

Röntgenstrahlung

elektromagnetisches Spektrum:



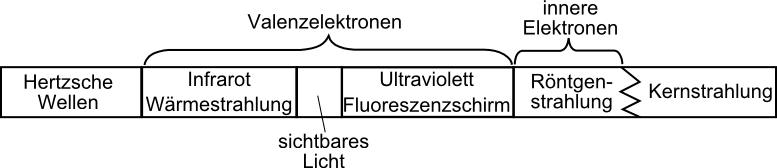
Röntgenspektrum:

  • niedrigste Energieniveaus im Atom frei ⇒ durch andere Elektronen der Atomhülle besetzt
  • Wellen im Bereich von 10-10m
  • Wellen an Atomen in Netzebenen gebeugt ⇒ interferieren
    • 2·a·sin φk = k·λ         a... Abstand der Netzebene
  • Elektronen treffen mit hoher Spannung UB auf die Anode
  • ⇒ Wechselwirkung ⇒ Energie als Strahlung abgegeben