Modelle und Grundgrößen
Notwendigkeit des Arbeitens mit Modellen:
- Vereinfachung der Realität
- Mittel zur Veranschaulichung
- Mittel zum Aufstellen, zum Weiterentwickeln und zum Anwenden einer Theorie
- Möglichkeit der Berechnung
Modell Massepunkt:
- Form und Volumen werden vernachlässigt
- Masse in einem Punkt konzentriert (mit dem Punkt wird der Ort betrachtet)
Relativität der Bewegung:
- Die Bewegung eines Körpers ist die Veränderung seines Ortes zu einem Bezugskörper
- Ein Körper ist in Ruhe, wenn er seinen Ort gegenüber einem Bezugskörper nicht ändert.
Grundgrößen:
Geschwindigkeit:
Die Geschwindigkeit gibt an, wie schnell sich ein Körper bewegt.Formelzeichen: v
Einheit: 1
ms
=3,6kmh

Unterscheidung der Bewegung nach:
Betrag der Geschwindigkeit:
| v = konstant gleichförmige Bewegung | v = veränderlich ungleichförmige Bewegung |
Richtung der Geschwindigkeit:
| geradlinige Bewegung | krummlinige Bewegung |
Gleichung der Momentangeschwindigkeit:
v =
ΔsΔt
=s2-s1t2-t1
mit Δt gegen 0Entgegengesetzte Bewegungen werden in einem Bezugssystem durch verschiedene Vorzeichen beschrieben.
genauer: v =
limΔ t→0
ΔsΔt
=dsdt
Geschwindigkeit als Anstieg im s(t)-Diagramm
Beschleunigung
Die Beschleunigung einer Bewegung ist die Geschwindigkeitsänderung Δv in dem Zeitintervall ΔtFormelzeichen: a
Einheit:
ms2
Gleichung: a =
ΔvΔt
=v2-s1t2-t1
mit Δt gegen 0Das Vorzeichen gibt wieder die Richtung der Änderung an.
Gleichförmige Bewegung
v = konstantGleichung: v =
Δst
Diagramme:
| s(t)-Diagramm | v(t)-Diagramm |
|---|---|
 | 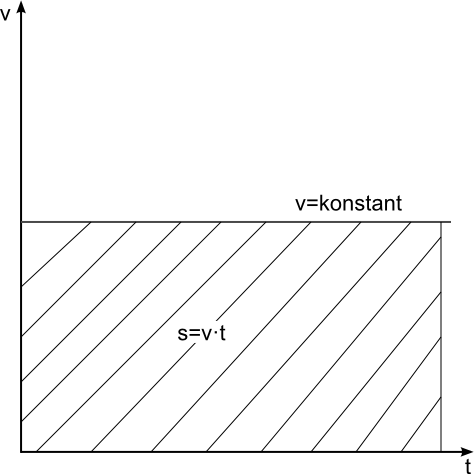 |
| Die Geschwindigkeit entspricht dem Anstieg im s(t)-Diagramm | Die Fläche unter der Kurve im v(t)-Diagramm entspricht dem zurückgelegten Weg |
Gleichmäßig beschleunigte Bewegung
a = konstantWeg-Zeit-Gesetz: s(t) =
as
·t2+v0·t+s0Geschwindigkeit-Zeit-Gesetz: v(t) = a·t+v0
Betrachtung der Beschleunigung:
| Vorgang | Geschwindigkeit | Beschleunigung |
|---|---|---|
| Anfahren | vA < vE | positiv |
| gleichförmige Bewegung | vA = vE | a = 0 |
| Bremsen | vA > vE | negativ |
Freier Fall:
Bedingungen:
- ohne Luftwiderstand
- v0 = 0
12
·g·t2Geschwindigkeit-Zeit-Gesetz: v(t) = g·t
Krummlinige Bewegung
Kreisbewegung:
| Modell Massepunkt Jede Kreisbewegung ist eine beschleunigte Bewegung gleichförmige Kreisbewegung 1 Umlauf ⇒ Weg = Kreisumfang Zeit = Umlaufzeit T v = 2·π·rT |  Kraft in Richtung Zentrum ⇒ Radialkraft (oder Zentripetalkraft) F = m·ar = m· v2r = m·4·π2·rT2 |
Kreisfrequenz (Winkelgeschwindigkeit):
Formelzeichen: ωEinheit: s-1
Gleichung: ω =
2·πT
=2·π·f = 2·π·nf... Frequenz in Hz
n... Drehzahl
Es folgt v = ω·r und Fr = m·ω2·r
| Analogie | Translation | Rotation |
|---|---|---|
| Weg s Geschwindigkeit v Beschleunigung a Newton'sches GG F = m·a Energie Ekin = 0,5·m·v2 | Drehwinkel φ Winkelgeschwindigkeit ω Winkelbeschleunigung M→ = r→× F→ M... Drehmoment Erot = 0,5·J·ω2 J... Trägheitsmoment |
Unabhängigkeitsprinzip:
Führt ein Körper mehrere Bewegungen in verschiedene Richtungen aus, so beeinflussen sich die Teilbewegungen gegenseitig nicht.Die Gesamtbewegung ergibt sich aus der vektoriellen Addition der Einzelbewegungen.schräger Wurf:
Überlagerung zweier Bewegungen:- x-Richtung gleichförmige Bewegung
- y-Richtung freier Fall
ay = -g
vx = v0·cos α = konstant
vy = -g·t+v0·sin α
x = v0·cos α·t
y = -0,5·g·t2+v0·sin α·t+h