Felder und Bewegung von Ladungsträgern

Systematisierung Feld

Unterschiede:

  elektrisches Feld magnetisches Feld
Beschreibung Das elektrische Feld ist der besondere Zustand des Raumes um elektrische Ladungen. Das magnetische Feld ist der besondere Zustand des Raumes um Dauermagneten und stromdurchflossene Leiter
Ursache elektrische Ladungen Dauermagnete
stromdurchflossene Leiter
Kräfte auf
  • geladene Körper
  • ungeladene Körper durch Polarisierung
  • Dauermagnete
  • stromdurchflossene Leiter
  • ferromagnetische Werkstoffe
Definition einer Feldgröße elektrische Feldstärke magnetische Flussdichte
Kraft auf Probekörper E =
F/Q
 B =
F/I·l

Gemeinsamkeiten:

  • besonderer Zustand des Raumes
  • Träger von Energie
  • an keine stofflichen Träger gebunden
  • lassen sich durch Kraftwirkung nachweisen

Feld Feldlinienbilder
real existierende Erscheinung
räumlich (3D)		 Modell, Vereinfachung
in einer Ebene (2D)
Das Feld existiert auch zwischen den Feldlinien

Das Feldlinienbild ermöglicht Aussagen über Richtung und Betrag der Kraft auf Probekörper
  1. Das Feld ist am stärksten, wenn die Feldlinien am dichtesten sind.
  2. homogenes Feld (Feld überall gleich stark) ⇒ Feldlinien parallel
  3. inhomogenes Feld (Feld unterschiedlich stark) ⇒ Feldlinien unterschiedlich dicht
  4. Richtung der Kraftwirkung auf positive Probeladungen/ Nordpole

Bewegung von Ladungsträgern in Feldern

  1. elektrisches Feld
    1. Ladungsträger parallel zu Feldlinien
      2. homogenes Feld
      ⇒gleichmäßig beschleunigte Bewegung
      Fel = Fmech
      E·Q = m·a
      a =
      U·Q/m·d
      Energiebetrachtung:
      sei v0 = 0 so gilt: Eel = Ekin             Q·U =
      1/2
      ·m·v2
    2. Ladungsträger senkrecht zu Feldlinien
      3. x-Richtung: gleichförmige Bewegung, v0 = konstant
      y-Richtung: beschleunigte Bewegung, "elektrische Wurfparabel"
      Fely = Fmech
      E·Q = m·ay
      vy = ay·t =
      Uy·Q/m·d
      ·t
      vges = √v02+vy2
  2. magnetisches Feld
    1. Ladungsträger parallel zu Feldlinien
      2. geradlinig gleichförmige Bewegung,
      weil Lorentzkraft FL = 0
    2. Ladungsträger senkrecht zu Feldlinien
      3. gleichförmige Kreisbewegung
      FL = Fr
      Q·v·B = m·
      v2/r

Massenspektrograph


d1 stellt den Durchmesser einer Kreisbahn dar. Die in der Skizze zu d1 gehörige Masse wäre m1.
  • Elektronenstrahl ionisiert Gasatome
  • Geschwindigkeitsfilter: elektrisches und magnetisches Feld stehe senkrecht zueinander ⇒ Ionen mit gleicher Geschwindigkeit werden erhalten
  • Fel übt Kraft nach unten auf positive Ionen aus
  • FL übt Kraft nach oben aus
  • ⇒ alle Ionen haben am Ende die gleiche Geschwindigkeit
  • B2 = homogenes Magnetfeld ⇒ zwingt Ionen auf eine Kreisbahn
  • Ionen treffen auf Fotoplatte ⇒ Bahnradius kann ermittelt werden ⇒ Bestimmung spezifische Ladung
  • ⇒ Ionenmasse kann bestimmt werden

Wirkungsweise:

  • Ionenquelle liefert Ladungsträger
  • Beschleunigung im elektrischen Feld
  • Energieerhaltungssatz:
    •   Eel = Ekin
    Q·U =
    1/2
    ·m·v2
    v = √
    2·Q·U/m
  • geradlinig gleichförmige Bewegung:
    •   Fel = FL
    Q·E = Q·v·B1
  • gilt für jene Teilchen mit v =
    E/B1
  • im Magnetfeld B2 gleichförmige Kreisbewegung
    •       FL = Fr
    Q·v·B = m·
    v2/r
  • Radius der Kreisbahn r =
    m·v/Q·B2
  • mit v aus Geschwindigkeitsfilter r =
    m·E/Q·B1·B2

Hall-Effekt

  • Körper im Magnetfeld ⇒ auf Ladungsträger wirkt Lorentzkraft
  • dünnes Metallband ⇒ Feldlinien senkrecht ⇒ Lorentzkraft führt dazu, dass sich Träger mit negativer Ladung in einem Punkt sammeln
  • zwischen diesem Punkt und entgegengesetztem ist Spannung messbar ⇒ Hall-Spannung
  • ⇒ Spannung wächst bis Kraft auf Ladungsträger = Lorentzkraft
    •                Fel = FL
    e·E = e·
    UH/b
    =e·v·B

Herleitung:

1. Annahme:

Es gibt nur eine Sorte von beweglichen Ladungsträgern (z.B. Elektronen) die zum Strom beitragen.

2. Annahme:

Alle queren mit der gleichen Geschwindigkeit v das Silberband:
      FL = Fel
Q·v·B = Q·E
Q·v·B = Q·
UH/b

     UH = v·B·b

Querstrom Iquer: Iquer =
Q/t
=
N·e/t
⇒t =
N·e/Iquer

Geschwindigkeit der Ladungsträger: v =
l/t
=
l·Iquer/N·e

Hallspannung: UH =
l·Iquer/N·e
·B·b =
l·b·d·Iquer·B/d·N·e

UH =
v·Iquer·B/N·e·d
=
1/n·e
·
Iquer·B/d

B =
n·e·d/I
·UH
n... Ladungsträgerdichte

Einteilung Naturkonstanten

universell Teilchen Feld
  • Lichtgeschwindigkeit
  • Plancksches Wirkungsquantum h
  • Elementarladung e
  • Masse Elektron me
  • Gravitationskonstante γ
  • elektrische Feldkonstante ε
  • magnetische Feldkonstante μ

Zusammenhänge: c = (√ε·μ  )-1

Milikan Experiment:

  • geladenes Teilchen zwischen horizontalen Kondensatorplatten
  • Elementarladung näherungsweise bestimmbar
  • unberücksichtigt Reibungskräfte und Auftriebskräfte
  • Radius r nicht direkt messbar (indirekt über die Sinkgeschwindigkeit eines Öltröpfchens ohne elektrisches Feld)

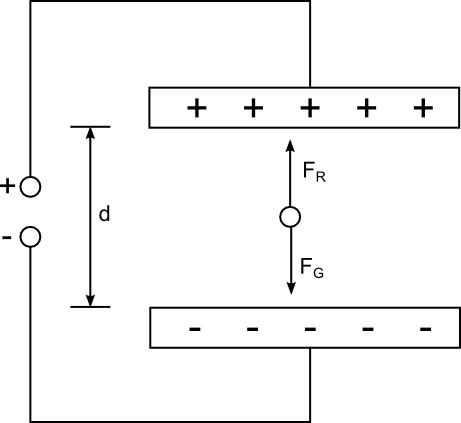Radiusbestimmung - Ansatz:

Kräftegleichgewicht: FG = FR
resultierende Kraft = 0 ⇒ gleichförmige Bewegung
kleine Geschwindigkeiten: Stokes'sche Reibung
m·g = 6·π·μ·r·v      mit       m = ρ·V =
4·π·r3·ρ/3

Radiusbestimmung:

r = 3·√
μ·v-/2·g·(ρÖl-ρLuft)

μ... Zähigkeit der Luft 1,8·10-5
kg/m·s

v-... Fallgeschwindigkeit ohne elektrisches Feld
ρÖl... Dichte des Öles = 910
kg/m3


Messgrößen:

  • Spannung am Kondensator im Schwebefall
  • Fallstrecke ohne Spannung
  • Fallzeit ohne Spannung

Fehlerbetrachtung:

  • Auftriebskräfte nicht berücksichtigt
  • Temperaturabhängigkeit der Konstanten nicht beachtet

Ergebnis:

Es häufen sich die ganzzahligen Vielfachen der Elementarladung. Die Ladung ist gequantelt.
e = 1,602·10-19 C als kleinste mögliche Ladung, da Q = k·e (ganzzahlig Vielfaches; k∈Z)

Bestimmung der spezifischen Ladung e/m:

Ansatz: Lorentzkraft = Radialkraft
     FL = Fr
e·v·B =
m·v2/r

   
e/m
=
v/B·r
    (1)

Beschleunigung im elektrischen Feld

Ansatz:
Eel = Ekin
e·U =
1/2
·m·v2
Gleichung (1) in Gleichung (2) einsetzen: e·U =
1/2
·m·
e2·B2·r2/m2

gekürzt: U =
1/2
·
e/m
·B2·r2
umgeformt:
e/m
=
2·U/B2·r2

U... Beschleunigungsspannung
r... Radius der Kreisbahn